TCTF/0CTF Rev Writeups

Writeups for Some 0CTF Challenges

vp

Once I opened the binary in ghidra I saw a clone which spawns a child after setting some seccomp rules and the parent just waits for that, so I went to the main function of the child and that just prints the welcome message, reads 0x68 bytes of input from the user, that gets copied into a global and we call another function before calling _exit(2)

Inside that another function, ghidra removed a few "unreachable" blocks... Which were reachable, so I right clicked, properties and unchecked the "eliminate unreachable code" in the Analysis Tab. Ghidra then decided to load for a moment before revealing a ton of code which consists of forks, then the child doing stuff in global memory (And the vforks share that memory space, so it affects the parent as well), while the parent just waits for it to die. We see that all the child processes just call _exit(2) at the end.

Then I spent a lot of time figuring out what all the globals do. At first I thought it was some sort of vm, because we first read a byte from an array (I assumed length of code), then we read three more bytes of that in a loop and did stuff with those bytes. As it turned out, that was not a vm, but more like constraints. The first byte was a direction (left, right, up, down). The second was the start position and the last byte was the expected result.

Now what do I mean with start position? Well, the first 100 bytes of the user input were used as a 10x10 grid. Then the direction was just in which direction we should go from our starting position. The starting position then was simply a number from one to ten indicating the row (for left, right) or column (for up, down). We then go through all ten fields in that row/column in the direction indicated by the first byte. While we do that, we check that every number from 1-10 occurs once as well as the number of times we get a new maximum along the way is the same as the third byte we have read from the array earlier.

So the first step was to solve this puzzle. I extracted the array of constants and parsed them, converting the data into data which needs less code to interpret (Starting position as absolute value from 0-100, direction converted to step size). Then I spent some time correctly implementing the constraints in z3. The script takes around 10 seconds, but finds a (i don't know if it's unique) solution to the quiz.

from z3 import *

arr = [BitVec(f"byte_{i}", 8) for i in range(100)]
s = Solver()
for i,x in enumerate(arr):
    s.add(x >= 0)
    s.add(x < 10)

    visible = []
    for j in range(10):
        if j!=i//10: visible.append(arr[(i%10)+j*10])
        if j!=i%10:  visible.append(arr[(i//10)*10+j])
    s.add(And(*[y != x for y in visible]))

s.add(arr[6] == 9)
s.add(arr[89] == 9)


def add_inversion_constraints(start, step, num, prev):
    if len(prev) == 10:
        return num == 0
    if num < 0:
        return False

    return And(
        Implies(
            And([arr[start] > x for x in prev]),
            add_inversion_constraints(start+step,step,num-1,prev+[arr[start]])
        ),
        Implies(
            And(Or([arr[start] < x for x in prev]), len(prev) > 0),
            add_inversion_constraints(start+step,step,num,prev+[arr[start]])
        )
    )

s.add(add_inversion_constraints(8,10,2,[]))
s.add(add_inversion_constraints(2,10,3,[]))
s.add(add_inversion_constraints(5,10,4,[]))
s.add(add_inversion_constraints(4,10,2,[]))
s.add(add_inversion_constraints(90,-10,2,[]))
s.add(add_inversion_constraints(93,-10,2,[]))
s.add(add_inversion_constraints(91,-10,4,[]))
s.add(add_inversion_constraints(97,-10,3,[]))
s.add(add_inversion_constraints(99,-10,2,[]))
s.add(add_inversion_constraints(30,1,2,[]))
s.add(add_inversion_constraints(40,1,2,[]))
s.add(add_inversion_constraints(90,1,3,[]))
s.add(add_inversion_constraints(70,1,3,[]))
s.add(add_inversion_constraints(20,1,2,[]))
s.add(add_inversion_constraints(19,-1,2,[]))
s.add(add_inversion_constraints(69,-1,3,[]))
s.add(add_inversion_constraints(59,-1,2,[]))
s.add(add_inversion_constraints(9,-1,2,[]))

s.add(arr[6] == 9)
s.add(arr[89] == 9)

if s.check() == sat:
    m = s.model()
    for i in range(10):
        for j in range(10):
            idx = i*10+j
            print(f"\\x0{hex(m[arr[idx]].as_long()+1)[2:]}",end="")
else:
    print("OOF")

gives us

\x08\x04\x01\x03\x09\x02\x0a\x06\x05\x07\x06\x02\x03\x08\x05\x04\x01\x07\x0a\x09\x09\x08\x0a\x06\x02\x05\x03\x01\x07\x04\x05\x01\x02\x04\x03\x0a\x07\x09\x06\x08\x02\x0a\x05\x09\x07\x03\x06\x08\x04\x01\x01\x07\x04\x05\x06\x09\x08\x0a\x02\x03\x0a\x03\x06\x07\x01\x08\x04\x05\x09\x02\x04\x09\x07\x0a\x08\x06\x02\x03\x01\x05\x03\x06\x09\x01\x04\x07\x05\x02\x08\x0a\x07\x05\x08\x02\x0a\x01\x09\x04\x03\x06

Interestingly enough, this sometimes produced Error sometimes Correct, I don't know why, I suspect some bad interleaving though.

So we solved the puzzle and can continue in our code. (Because if it wasn't correct, we just print "Error :(" and _exit(2)). The rest of the code was pretty small, still took quite some time to figure out that it just takes the four extra bytes we sent (0x68 == 104), splits them into to shorts, takes one as an offset into the array (Which coincidentally is right before the stack). So we only have to overwrite the return address to jump to the win function which reads the flag file (After doing some xoring to obfuscate the string "flag"). This function has the low two bytes of 0x0cc8, so we get \xc8\x0c as value to write (Little endian) and we just have to get the correct offset into the stack. During the clone call in the main function, we set the stack to be at address 0x30c0c0, while the array starts at address 0x304020. That means that our stack is at most at offset 0x80a0. So I tried a few different addresses from there on down in increments of 8. On my local machine the address 0x8008 always worked, on the remote it worked in like 1 out of 30 tries. But it worked and we got the flag by doing the thing in a while loop lol

while true; do echo -e "\x08\x04\x01\x03\x09\x02\x0a\x06\x05\x07\x06\x02\x03\x08\x05\x04\x01\x07\x0a\x09\x09\x08\x0a\x06\x02\x05\x03\x01\x07\x04\x05\x01\x02\x04\x03\x0a\x07\x09\x06\x08\x02\x0a\x05\x09\x07\x03\x06\x08\x04\x01\x01\x07\x04\x05\x06\x09\x08\x0a\x02\x03\x0a\x03\x06\x07\x01\x08\x04\x05\x09\x02\x04\x09\x07\x0a\x08\x06\x02\x03\x01\x05\x03\x06\x09\x01\x04\x07\x05\x02\x08\x0a\x07\x05\x08\x02\x0a\x01\x09\x04\x03\x06\xc8\x0c\x08\x80"|nc 111.186.59.32 20217 ; done

eventually gave us

flag{vvvvvfork_is_good_to_play_a_skycraper^.^}

FA51R_re

The gist of this challenge was that each function was in it's own file. So I just sorted the files by size and started reversing. Sometimes I decided to use the help of gdb to do some dynamic testing. For that I set a breakpoint in dyn_call and looked at the stack. Then I just continued until the correct function-name was there.

Well, anyway the smaller functions were pretty easy to reverse, so I just commented on their functionality in a file

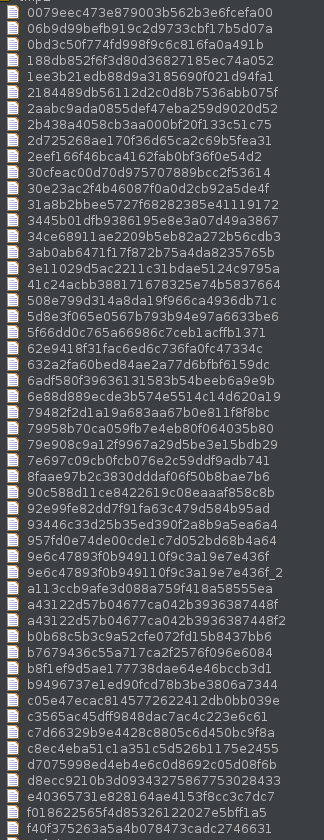
06b9d99befb919c2d9733cbf17b5d07a      is help ==> just a bunch of puts() calls
0bd3c50f774fd998f9c6c816fa0a491b      password_check();
188db852f6f3d80d36827185ec74a052      return (shm[0x120] = shm[0x120] * 0x41c64e6d + 0x3039 & 0x7FFFFFFF); // bitwise after addition/mult
1ee3b21edb88d9a3185690f021d94fa1      syscall, 1 argument (apart from number, sysnum in rdi, arg in rsi)
2184489db56112d2c0d8b7536abb075f      prints the hello message (Just a wrapper for print)
2b438a4058cb3aa000bf20f133c51c75      wrapper for 1ee3b21edb88d9a3185690f021d94fa1(3, arg1) ==> close(fd)
2d725268ae170f36d65ca2c69b5fea31      syscall --> arguments are like this: rax=rdi, rdi=rsi, rsi=rdx, rdx=rcx (so just shift them)
2eef166f46bca4162fab0bf36f0e54d2      arg<<4 | arg >> 0xC ==> swap nibbles?
2aabc9ada0855def47eba259d9020d52      wrapper for 62e9 ==> syscall 2, arg1, arg2 ==> open(arg1, flags)
30cfeac00d70d975707889bcc2f53614      strcpy(arg1, arg2) == strcpy(dst, src)
31a8b2bbee5727f68282385e41119172      check if arg not in range(14, 32) ==> return arg == 32 || arg<14 ==> whitespace characters?
3445b01dfb9386195e8e3a07d49a3867      admin's menu option ==> same loop as before, but we don't have the binaries for those...
34ce68911ae2209b5eb82a272b56cdb3      3ab0(read_line(local_buf, 0x14));
3ab0ab6471f17f872b75a4da8235765b      strtol (string to int conversion), arg1 buf, arg2 len, returns int
3e11029d5ac2211c31bdae5124c9795a      move bits through array? ==> see code transcript below
508e799d314a8da19f966ca4936db71c      strlen(char*src) -> int
5d8e3f065e0567b793b94e97a6633be6      is admin's password option
5f66dd0c765a66986c7ceb1acffb1371      return 0x96 < shm[4] (shm is a ushort*)
62e9418f31fac6ed6c736fa0fc47334c      syscall, 2 extra args
632a2fa60bed84ae2a77d6bfbf6159dc      is_digit(char num) -> bool ==> return param-0x10<10
6adf580f39636131583b54beeb6a9e9b      weird bit checks?
6e88d889ecde3b574e5514c14d620a19      ret (... the file is two bytes, what did you expect?)
79482f2d1a19a683aa67b0e811f8f8bc      print_menu(); // just a bunch of puts
79e908c9a12f9967a29d5be3e15bdb29      write(1, arg1, strlen(arg1)); // puts?
7e697c09cb0fcb076e2c59ddf9adb741      get_flag
8faae97b2c3830dddaf06f50b8bae7b6      2d72(0, arg1, arg2, arg3) ==> read(arg1, arg2, arg3) # fd, buf, num
90c588d11ce8422619c08eaaaf858c8b      int_to_str (buf, num) --> ptr into buf, where num_str begins
92e99fe82dd7f91fa63c479d584b95ad      int x = 188d(); return c8ec(x&0xF,x>>4);
93446c33d25b35ed390f2a8b9a5ea6a4      syscall (but no arguments apart from the syscall number; syscall number in rdi)
9e6c47893f0b949110f9c3a19e7e436f      main_loop
d7075998ed4eb4e6c0d8692c05d08f6b      ??? first in check_password ==> print timestamp & write that to global 0x120 ==> short index 0x90
b7679436c55a717ca2f2576f096e6084      exit(arg1), another wrapper
b8f1ef9d5ae177738dae64e46bccb3d1      login ==> if 0bd3(arg1, arg2) {print("yay"); return 1;} else {print("nay"); return 0;}
b9496737e1ed90fcd78b3be3806a7344      time (2d725268ae170f36d65ca2c69b5fea31(0xc9, 0, 0, 0) --> syscall time())
c05e47ecac8145772622412db0bb039e      read_line(buf, max_len) // reads max_len or until null or newline
c7d66329b9e4428c8805c6d450bc9f8a      shm[0x120] = param (DWORD)
c8ec4eba51c1a351c5d526b1175e2455      return (arg1 << (4 * arg3)) | ((short*)rodata)[arg2] << arg4  // i actually don't know if this is correct...
b0b68c5b3c9a52cfe072fd15b8437bb6      syscall (6 extra parameters?)
d8ecc9210b3d09343275867753028433      2d72(1, arg1, arg2, arg3) ==> write(arg1, arg2, arg3) # fd, buf, num
f018622565f4d85326122027e5bff1a5      syscall with more args (8 xmmwords on the stack, but only if al!=0)
f40f375263a5a4b078473cadc2746631      wrapper for syscall 0x3c ==> exit(arg1)

The main program also provides some rodata at address 0x600000000 and a shared memory space at address 0x700000000. After looking long enough that seemed to be a bunch of shorts at offset 0x1a8. As well as an int at offset 0x120. When we selected the login option from the menu, that was initialized to the timestamp and then used as seed for a basic prng.

Going through the binaries in order of their size made it really easy, because either we only do basic stuff or stuff that's already reversed or it's a wrapper for a bigger file, which is also quite easy.

For some of the files I wrote some pseudo C to better understand them:

code_3e11029d5ac2211c31bdae5124c9795a:
    extern short *shm; // shared memory
    for(int i = arg1; arg1 > 0; arg1--) {
        shm[0xd4 + i] & ~arg2;
        shm[0xd4 + i] |= (shm[0xd3 + i] & arg2);
    }

code_6adf580f39636131583b54beeb6a9e9b:
    extern short *shm; // shared memory
    for(int i = 0; i < 4; i++) {
        if(shm[0xd5 + i] & arg1) {
            shm[0xd4 + i] |= arg1;
            return;
        }
    }
    shm[0xd8] |= arg1;


code_e40365731e828164ae4153f8cc3c7dc7:

    short x = arg1;
    for(int i = 0; i < 4; i++) {
        if(arg2 >> (i + 4)) x = x>>4 | x<<0xc;
    }
    for(int i = 0; i < 4; i++) {
        if(arg2 >> i) x = (x>>3 & 0x1111) | (x<<1 & 0xeeee);
    }
    return x;

code_30e23ac2f4b46087f0a0d2cb92a5de4f:
    int i = 4;
    while(i) {
        bool x = false; // needs to be false to go to next index

        ushort loc = shm[0xd4+i];
        for(int j = 0; j < 4; j++) {
            if((loc >> (j*4)) & 0xF == 0xF) {
                x = true;
                shm[4]++;
                code_3e11(i, 0xF << (4 * j));
                loc = shm[0xd4+i];
            }
        }
        for(int j = 0; j < 4; j++) {
            if(loc & (0x1111 << j) == (0x1111 << j)) {
                x = true;
                shm[4]++;
                code_3e11(i, 0x1111 << j);
                loc = shm[0xd4+i];
            }
        }

        if(!x) i--;
    }

code_41c24acbb388171678325e74b5837664:
    int loc = 0;
    while(loc < arg2 && shm[4] <= 0x96) {
        int x = arg1[loc];
        int y = code_92e9(); // int x = 188d(); return c8ec(x&0xF,x>>4);
        957f(x, y);
        loc++;
    }
    return 0;

code_957fd0e74de00cde1c7d052bd68b4a64:
    short var1 = e403(arg2, arg1);
    code_6adf(var1);
    code_a113();
    code_30e2();
    return 0;

code_d7075998ed4eb4e6c0d8692c05d08f6b: // init_timestamp()
    int t = time(arg1, arg2);
    puts("Timestamp: ");
    puts(int_to_str(t));
    puts("\n");
    code_c7d6(t);

code_0bd3c50f774fd998f9c6c816fa0a491b: // password_check
    code_d707(arg1, arg2); // init_timestamp();
    puts("input> ");
    read_line(loc_418, 1000);
    int len = strlen(loc_418);
    code_41c2(loc_418, len); // actual password check here
    return shm[4] > 0x96; // all characters passed the checks?

I also looked at the admin pw and flag options, but since I needed to login to access those I decided to not look into them further (I mean they probably just read the corresponding file and print the contents).

So I started in the login function, that just gets the time, prints that and sets the seed in the shared memory. Then I continued into the actual "password" check. I quickly realized that the login is not really a password since we never check anything about that without introducing some random into it.

So I started taking notes what actually was checked. since code_6adf580f39636131583b54beeb6a9e9b is called with every of our inputs we see that the array is slowly growing downards (if the numbers share the same bits). And we had to prevent this array to grow more than 4 places down.

Next I looked at code_3e11029d5ac2211c31bdae5124c9795a that moves the bits downards and clears the ones in the short at offset start.

Next code_30e23ac2f4b46087f0a0d2cb92a5de4f does checks on all the shorts in the array, those checks being if either all bits in a nibble are 1 or if in all four nibbles in the short the same bit is set. If that is the case then we call the function to clear the bits.

After that I spent too much time implementing the code in python to simulate the game... twice. Luckily I did it twice as obviously there were some minor bugs.

First I implemented the piece generation which takes a random value and generates a piece based on a constant from rodata shifted by an amount and oring some other part of the random value.

data = [
            0x0000,
            0x0001,
            0x0010,
            0x0011,
            0x0100,
            0x0101,
            0x0110,
            0x0111,
            0x1000,
            0x1001,
            0x1010,
            0x1011,
            0x1100,
            0x1101,
            0x1110,
            0x1111
        ]

def transform_value(a, b, c, d):
    return (a << (c << 2)) | (data[b] << d)

def transform_random_value(x):
    # random value ==> takes nibbles and third nibble in two two-bit values and gives that to transform_values
    return transform_value(x & 0xf, (x >> 4) & 0xf, (x >> 8 & 3), ((x >> 8) & 0xf) >> 2)

seed = 0x60e14dee # testing seed, change later
def rand(): # PRNG seeded by the timestamp
    global seed
    seed = (seed * 0x41c64e6d + 0x3039) & 0x7FFFFFFF
    return seed

def mutate_char_based_on_random_variable(x, y):
    for i in range(4):
        if (y >> (i + 4)) & 1 == 1:
            x = (x>>4 | x<<0xc) & 0xFFFF
    for i in range(4):
        if (y >> i) & 1 == 1:
            x = ((x>>3 & 0x1111) | (x<<1 & 0xeeee)) & 0xFFFF
    return x

now by calling mutate_char_based_on_random_variable(transform_random_value(rand()), user_input) I could get the correct output...

So I wrote a simple bot which does not always work (It hangs itself because it can't find any good moves anymore). But it succeeds sometimes. It worked on both my implementations in python, but not on the binary.

It's always the dumb mistakes. And for this I made the beginning at the very beginning. In code_e40365731e828164ae4153f8cc3c7dc7 during the first loop I swapped the >> and the << (it actually calls 2eef166f46bca4162fab0bf36f0e54d2 for which I actually have the right code written right next to it.. But for some reason I failed to copy that down)

Anyhow, after fixing that my bot also worked correctly on the binary, so all I had to do was to run it on the remote. Once it found a solution I was able to get the flag and the admin password (Which was ultimately not used in our team).

Here the full solve script:

data = [
            0x0000,
            0x0001,
            0x0010,
            0x0011,
            0x0100,
            0x0101,
            0x0110,
            0x0111,
            0x1000,
            0x1001,
            0x1010,
            0x1011,
            0x1100,
            0x1101,
            0x1110,
            0x1111
        ]

seed = 0x60e14dee
shm = [0 for i in range(0x100)] # short array

def rand(): # PRNG seeded by the timestamp
    global seed
    seed = (seed * 0x41c64e6d + 0x3039) & 0x7FFFFFFF
    return seed

def mutate_char_based_on_random_variable(x, y):
    for i in range(4):
        if (y >> (i + 4)) & 1 == 1:
            x = (x<<4 | x>>0xc) & 0xFFFF;
    for i in range(4):
        if (y >> i) & 1 == 1:
            x = ((x>>3 & 0x1111) | (x<<1 & 0xeeee)) & 0xFFFF;
    return x

def mutate_state(value):
    global shm
    for i in range(4):
        if(shm[0xd5 + i] & value) != 0:
            shm[0xd4 + i] |= value
            return
    shm[0xd8] |= value

def check_cond():
    global shm
    if shm[0xd4] != 0:
        return False
    return True

def code_3e11(start, value):
    global shm
    for i in range(start,0,-1):
        shm[0xd4 + i] &= (~value)
        shm[0xd4 + i] |= (shm[0xd3 + i] & value)


def do_stuff_based_on_state():
    i = 4
    while i > 0:
        x = False
        loc = (shm[0xd4+i] & 0xFFFF)
        for j in range(4):
            if (loc >> (j*4)) & 0xF == 0xF:
                x = True
                shm[4] += 1
                code_3e11(i, (0xF << (4 * j)) & 0xFFFF)
                loc = shm[0xd4+i]
        for j in range(4):
            if loc & (0x1111 << j) == (0x1111 << j):
                x = True
                shm[4] += 1
                code_3e11(i, (0x1111 << j) & 0xFFFF)
                loc = shm[0xd4+i]

        if not x:
            i -= 1

xx = 0
def check_stuff(x, y):
    global xx
    var1 = mutate_char_based_on_random_variable(y, x)
    #print(f"{var1 = } ({xx}. char)")
    print(var1,end=",")
    xx += 1
    mutate_state(var1)
    if not check_cond(): return False
    do_stuff_based_on_state()
    return True

def check_stuff_with_mutated_value(var1):
    mutate_state(var1)
    if not check_cond(): return False
    do_stuff_based_on_state()
    return True


def transform_value(a, b, c, d):
    return (a << (c << 2)) | (data[b] << d);

def transform_random_value(x):
    # random value ==> takes nibbles and third nibble in two two-bit values and gives that to transform_values
    return transform_value(x & 0xf, (x >> 4) & 0xf, (x >> 8 & 3), ((x >> 8) & 0xf) >> 2)

def check_password(password):
    global shm
    for i in range(len(password)):
        x = (password[i])
        y = transform_random_value(rand())
        if not check_stuff(x,y): 
            for i in range(5):
                print(f"{i} ==> {hex(shm[0xd4+i])}")
            print(f"Failed at character {i} == {(password[i])}")
            return i
        if shm[0x4] > 0x96:
            print("GOT IT")
            print(password)
            break
    print(shm[4])
    return len(password)

"""
check_stuff_with_mutated_value(0b000000000001001)
check_stuff_with_mutated_value(0b000000000001011)
for i in range(5):
    print(f"{i} ==> {shm[0xd4+i]}")
check_stuff_with_mutated_value(0b0000000000000001)
for i in range(5):
    print(f"{i} ==> {shm[0xd4+i]}")
check_stuff_with_mutated_value(0b0000000000000110)
for i in range(5):
    print(f"{i} ==> {shm[0xd4+i]}")
"""

def undo():
    r = transform_random_value(rand()) # get random value for current char

    vals = set()
    for j in range(256):
        x = r&0xFFFF
        for i in range(4):
            if (j >> (i + 4)) & 1 == 1:
                x = (x<<4 | x>>0xc) & 0xFFFF
        for i in range(4):
            if (j >> i) & 1 == 1:
                x = ((x>>3 & 0x1111) | (x<<1 & 0xeeee)) & 0xFFFF
        """
        for i in range(4):
            if (0xF<<(4*i))&x == (0xF<<(4*i)):
                x &= ~(0xF<<(4*i))
        for i in range(4):
            if (0x1111 << i) & x == (0x1111<<i):
                x &= (~(0x1111<<i))
        """
        vals.add((r,x))
    return sorted(list(vals))
def brute(r, y):
    for j in range(256):
        x = r&0xFFFF
        for i in range(4):
            if (j >> (i + 4)) & 1 == 1:
                x = (x<<4 | x>>0xc) & 0xFFFF
        for i in range(4):
            if (j >> i) & 1 == 1:
                x = ((x>>3 & 0x1111) | (x<<1 & 0xeeee)) & 0xFFFF
        """
        for i in range(4):
            if (0xF<<(4*i))&x == (0xF<<(4*i)):
                x &= ~(0xF<<(4*i))
        for i in range(4):
            if (0x1111 << i) & x == (0x1111<<i):
                x &= (~(0x1111<<i))
        """
        if x == y:
            return [j]

    print("Not found")
    exit(101)


from pwn import remote, process, gdb
rem = remote("111.186.58.164", 30333)
#rem = process("./main")
#rem = gdb.debug(["./main"])
x = rem.recvuntil("name:")
rem.sendline("admin")
rem.recvuntil("choice: ")
rem.sendline("1")
rem.recvuntil("Timestamp: ")
timestamp = int(rem.recvline().strip())
seed = timestamp

#seed = 1625387938
state = [0 for i in range(5)]
p = [undo() for i in range(1000)]

def evaluate_move(value, simulate=True):
    global state
    st = state.copy()
    placed = False
    for i in range(4):
        if(st[i+1] & value) != 0:
            st[i] |= value
            placed = True
            break
    if not placed:
        st[4] |= value
    removed_pieces = 0
    i = 4
    while i > 0:
        x = False
        loc = st[i] & 0xFFFF
        for j in range(4):
            value = 0xF<<(j*4)
            if loc & value == value:
                x = True
                removed_pieces += 1
                for k in range(i,0,-1):
                    st[k] &= (~value)
                    st[k] |= (st[k-1] & value)
                loc = st[i]
        for j in range(4):
            value = (0x1111 << j)
            if loc & value == value:
                x = True
                removed_pieces += 1
                for k in range(i,0,-1):
                    st[k] &= (~value)
                    st[k] |= (st[k-1] & value)
                loc = st[i]
        if not x:
            i -= 1

    zb = sum([1 if x == 0 else 0 for x in state])
    za = sum([1 if x == 0 else 0 for x in st])
    if not simulate:
        state = st
        return removed_pieces
    return removed_pieces + (za-zb)



bias = 5
score = 0
inp = []
vals = []
for idx,v in enumerate(p):
    moves = [[] for i in range(10)]
    maxval = 0
    for r,x in v:
        val = evaluate_move(x)+bias
        moves[val].append((r,x))
        maxval = max(maxval, val)
    making_move = moves[maxval][0]

    score += evaluate_move(making_move[1], False)
    inp += brute(making_move[0], making_move[1])
    vals.append(making_move[1])

    print(hex(making_move[1])[2:].rjust(4,'0'),end=" ==> ")
    print([hex(x)[2:].rjust(4,'0') for x in state])
    if score > 160:
        ii = inp
        inp = []
        for x in ii:
            if x == 0:
                x = 0xF0
            elif x == 10:
                x = 5
            inp.append(x)
        print(inp)
        print(timestamp)
        print(vals)
        seed = timestamp
        check_password(bytes(inp))
        with open("testinput", "wb") as f:
            f.write(bytes(inp))
        rem.sendline(bytes(inp))
        rem.interactive()
        exit(0)

Gives us the flag flag{0ops! Dock menu overflow detected!afb11f59398789a08a3e5e60690d6726e5c5c1e1} which seems like a weird flag to me, maybe it's a hint for the pwn part.

future (Leo did all the important work lol)

This binary used intel's new extension AMX which will be released on some server CPUs this year. Neither ghidra, binary ninja, nor IDA could reverse those instructions, luckily enough objdump could "correctly" translate the instructions. It failed at the arguments as we later learned however (mixing up stride and size with an offset)

At least IDA/Ghidra could decompile some functions, which were used to check the output of the computation. Namely the function at 0x4010960, which just compares 64 bytes, 0x4019d0 which checks that two float arrays are the same (each having 64 entries) and 0x401a80 doing the same but with unsigned int arrays. And 0x401b10 doing the same but comparing a float array with a 16 bit float array (16 bit like the ones used by the intel spec which are just 32 bit floats but only 7 bits mantissa, so much less precision)

Then we had to look at the main function located at 0x401bb0. We could look at the parts between the AMX instructions in ghidra/IDA to get a better understanding of them. Those pretty much just convert from a 32 bit integer array to a 16 bit float array. And then it nulls out the second part of the 256 bytes (so setting the floats to zero basically)

  if (0 < height) {
    iVar3 = 0;
    iVar4 = 0;
    iVar2 = 0;
    do {
      if (0 < width_in_bytes) {
        lVar1 = 0;
        do {
            // not sure about indices but I guess it just converts all the input at param_2 to floats and stores them at short_arr
          short_arr[2*iVar4 + lVar1/2] = (short)((uint)(float)*(int *)(param_2[lVar1 + iVar3/4]) >> 0x10); // store every second float
          lVar1 = lVar1 + 4;
        } while (lVar1 < width_in_bytes);
        iVar4 = iVar4 + (width_in_bytes - 1U >> 2) + 1; // += 0x10, width_in_bytes is 0x20
      }
      iVar2 = iVar2 + 1;
      iVar3 = iVar3 + width_in_bytes;
    } while (height != iVar2);
  }
  // Clear out where we got our data from
  for (lVar1 = 0x80; lVar1 != 0; lVar1 = lVar1 + -1) {
    *param_2 = 0;
    param_2 = param_2 + 1;
  }

After manually decoding the tile config, we saw that only tile two was a 8 by 8 32-bit integer matrix which just contains the bits when unhexing the first 16 chars of our input. All other tiles are just 1x8 vectors.

This matrix then gets multiplied by the unit vector, that vector gets multiplied by tile two and added to the data already there, so basically we have

tmp += tmp * (BM + I)

Where BM is our input Bitmatrix and I is the identity 8x8 matrix. This gets repeated 4 times, after every time the data gets converted to floats and stored somewhere in memory. Then at address 0x4020d0 this process is over and we have the first few rows, the rest then gets filled up with the same as the 5th row (so row 5 through 8 all contain the same data). Then we load some constants, do one last matrix multiplication with floats this time and call the comparing function. So clearly we just have to find a matrix for which this check will succeed.

So we first dumbed all the constants (Which were luckily all formatted the same way, with the movabs instruction) with a quick grep movabs future.s | cut -d" " -f3 | cut -d"," -f2 on the objdump code. Then we used

f16arr = []
for i in values[32:]:
    print(hex(i))
    for j in range(4):
        print((i >> (16 * j)) & 0xFFFF)
        v = unpack("f", b"\x00\x00"+pack("H", (i >> (16 * j)) & 0xFFFF))[0]
        f16arr.append(v)

f32arr = []
for i in values[:32]:
    hi = i>>32
    lo = i&(1<<32)-1
    hi = unpack("f", pack("I", hi))[0]
    lo = unpack("f", pack("I", lo))[0]
    f32arr.append(lo)
    f32arr.append(hi)

to convert the values to the required formats. So we had 64 32-bit floats and 128 16-bit floats, which were stored in pairs of 2, so we had to get the two submatrices, one of which is multiplied by zero. The other is multiplied by our Result matrix built from the tmp results, the two results are then added, which means we don't have to worry about half of the constants (Every second will suffice)

So we can write this script to get the expected resulting matrix:

s=[0.099609375, 1.796875, 3.5, 5.1875, 6.875, 8.5625, 10.25, 12.0, 13.6875, 15.375, 17.0, 18.75, 20.5, 22.125, 23.875, 25.5, 0.3984375, 2.09375, 3.796875, 5.5, 7.1875, 8.875, 10.5625, 12.25, 14.0, 15.6875, 17.375, 19.0, 20.75, 22.5, 24.125, 25.875, 0.69921875, 2.390625, 4.09375, 5.78125, 7.5, 9.1875, 10.875, 12.5625, 14.25, 16.0, 17.625, 19.375, 21.0, 22.75, 24.5, 26.125, 1.0, 2.6875, 4.375, 6.09375, 7.78125, 9.5, 11.1875, 12.875, 14.5625, 16.25, 18.0, 19.625, 21.375, 23.0, 24.75, 26.5, 1.296875, 3.0, 4.6875, 6.375, 8.0625, 9.75, 11.5, 13.1875, 14.875, 16.5, 18.25, 20.0, 21.625, 23.375, 25.0, 26.75, 1.59375, 3.296875, 5.0, 6.6875, 8.375, 10.0625, 11.75, 13.5, 15.1875, 16.875, 18.5, 20.25, 22.0, 23.625, 25.375, 27.0, 1.8984375, 3.59375, 5.28125, 7.0, 8.6875, 10.375, 12.0625, 13.75, 15.5, 17.125, 18.875, 20.5, 22.25, 24.0, 25.625, 27.375, 2.1875, 3.890625, 5.59375, 7.28125, 9.0, 10.6875, 12.375, 14.0625, 15.75, 17.5, 19.125, 20.875, 22.5, 24.25, 26.0, 27.625]

e=[5483.724609375, 8271.57421875, 6230.849609375, 6473.162109375, 7995.32421875, 8923.44921875, 7128.099609375, 8612.724609375, 5574.630859375, 8408.357421875, 6333.333984375, 6579.833984375, 8128.279296875, 9071.591796875, 7244.537109375, 8755.193359375, 5661.162109375, 8538.517578125, 6430.818359375, 6681.318359375, 8254.861328125, 9212.611328125, 7355.224609375, 8890.787109375, 5760.662109375, 8688.287109375, 6543.162109375, 6798.193359375, 8400.287109375, 9374.693359375, 7483.037109375, 9046.787109375, 5842.724609375, 8811.583984375, 6635.537109375, 6894.349609375, 8520.271484375, 9508.333984375, 7587.849609375, 9175.349609375, 5941.224609375, 8960.068359375, 6746.849609375, 7010.162109375, 8664.318359375, 9668.943359375, 7714.599609375, 9329.724609375, 6032.099609375, 9096.841796875, 6849.318359375, 7116.818359375, 8797.248046875, 9817.060546875, 7831.037109375, 9472.162109375, 6118.662109375, 9227.005859375, 6946.818359375, 7218.318359375, 8923.849609375, 9958.099609375, 7941.724609375, 9607.787109375]


s1=s[0::2]
s2=s[1::2]

s1=[s1[i*8:i*8+8] for i in range(8)]
s2=[s2[i*8:i*8+8] for i in range(8)]
e=[e[i*8:i*8+8] for i in range(8)]

s1=Matrix(s1).transpose()
s2=Matrix(s2).transpose()
e=Matrix(e).transpose()

# x * s1 == e
# ==> e * s1.inverse() == x

r = flatten([[(y) for y in x] for x in (e*s1.inverse())])

print(r)

Now just a quick z3 script to get the correct input we need to have:

from z3 import *

def mult(d, x, y):
    for i in range(8):
        for k in range(8):
            d[i] += x[k] * y[k*8+i]

R = [
    0, 1, 0, 0, 1, 1, 0, 0,
    2, 1, 1, 1, 2, 2, 0, 2,
    4, 8, 4, 5, 8, 9, 4, 6,
    19,25,19,20,27,29,19,30,
    70,106,80,83,102,114,92,110,
    70,106,80,83,102,114,92,110,
    70,106,80,83,102,114,92,110,
    70,106,80,83,102,114,92,110,
]

s = Solver()
y = [Int(f"{i}") for i in range(64)]
for i, x in enumerate(y):
    s.assert_and_track(Or(x == 0, x == 1), f"{i}_one_zero")

x = [0 if i > 0 else 1 for i in range(8)]
t = [0 for i in range(8)]

for j in range(5):
    mult(t, x, y)
    tmp = x
    x = t
    t = tmp
    for i in range(8):
        s.assert_and_track(x[i] == R[i+j*8], f"{i}_{j}_R")


if s.check() == sat:
    m = s.model()
    vals="".join([str(m[x].as_long()) for x in y])
    print(vals)
else:
    print("OOF")

Then we only had to combine the bits, remember the endianess and get 328059c335ba44ee.

For the second part we simply had to extract the constants which were already captured by the grep earlier, then had to interpret them as floats. The second part was pretty easy as all it did was load the rest of the flag, unhexes them, each byte being one entry in a matrix. Then we do a packed dot product with constants, and each byte being quadrupled. This also needed to result in a constant matrix, so we could pretty easily reverse that:

s=[
    0x792d,
    0x57e4,
    0x5557,
    0x4d46,
    0x213f,
    0x42e7,
    0x35ce,
    0x4387,
    0x7270,
    0x5084,
    0x5b24,
    0x466c,
    0x2729,
    0x3472,
    0x3a6e,
    0x4c62,
    0x581b,
    0x44a2,
    0x426e,
    0x3d9a,
    0x1493,
    0x3632,
    0x3032,
    0x2f30,
    0x7684,
    0x4b5a,
    0x4731,
    0x4361,
    0x206a,
    0x3f34,
    0x3953,
    0x4814,
    0x6d16,
    0x3ffe,
    0x4b08,
    0x40c7,
    0x1f09,
    0x334b,
    0x3af5,
    0x47a0,
    0x683b,
    0x549e,
    0x504d,
    0x453b,
    0x1ea6,
    0x3c19,
    0x35aa,
    0x3c18,
    0x68e6,
    0x4abd,
    0x4ded,
    0x4169,
    0x1c3a,
    0x374a,
    0x359f,
    0x4102,
    0x6e85,
    0x4e31,
    0x4924,
    0x3f49,
    0x219d,
    0x394a,
    0x308a,
    0x44c8
]

r=[143742850,
 1500679553,
 1213089849,
 2371309128,
 1259016573,
 520656013,
 1149119617,
 2350613097,
 2469235085,
 1059140166,
 1115291789,
 2055836527,
 2303167263,
 607136286,
 224233739,
 593263665,
 306389906,
 2503681068,
 1394641664,
 289080374,
 823868953,
 1763860601,
 2440656165,
 857621294,
 1582268986,
 930304874,
 1886357596,
 2186617869,
 1125732242,
 740190819,
 1174611273,
 1352020864,
 2204250751,
 2467299341,
 831750976,
 1849887034,
 1999338643,
 258539567,
 723225355,
 1262439038,
 2090227780,
 2085843224,
 931013460,
 1847889741,
 17236616,
 2037847101,
 1754286365,
 705512785,
 2452696378,
 1245857567,
 1902850600,
 1732658203,
 1041465451,
 2241020698,
 460524438,
 627463481,
 327683886,
 2187220237,
 1868895109,
 1818457928,
 2454593061,
 2049339708,
 409810433,
 1680381313]

s=[[j for j in s[i*8:i*8+8]] for i in range(8)] # make it 8x8
r=[[(j&0xFF) + ((j>>8) & 0xFF) + ((j>>16) & 0xFF) + ((j>>24) & 0xFF) for j in r[i*8:i*8+8]] for i in range(8)] # add the bytes, because each int is actually a pair of 4 bytes
s=Matrix(s)
r=Matrix(r)
print("".join(flatten([[hex(int(y))[2:] for y in x] for x in (r.inverse()*s)])))

now we only had to combine them to get the full flag of flag{328059c335ba44eef6bc269996101901bb046bd87fe49118d0e2308ecda708487bee2790f11c2506)